Samples, Populations, and their Symbols
Terminology
Samples come from populations, and represent a smaller subset of all possible values.
- e.g. If you email 100 clients at random from a list of 10,000 clients.
Statistics describe samples whereas parameters describe populations (alliteration, FTW)
- e.g. The “average age of all clients” vs “average age of the 100 clients we selected”
Symbols
Generaly, Greek tends to mean population, whereas things with hats tend to mean sample.
# cheating because rendering table w/ latex
# in jupyter and hugo is a headache
from IPython.display import Image
Image(filename='../images/symbol_table.png')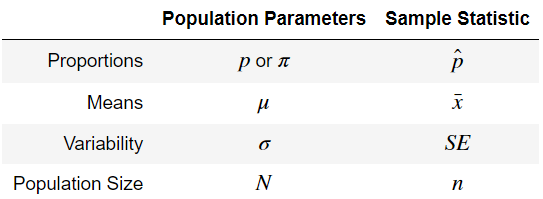
Calculating Sample Statistics
Proportions
Sample Proportion
$$\hat{p} = \frac{\text{Number of successes}}{\text{sample size}}= \frac{X}{n}$$
Standard Error
$$SE_\hat{p} = \sqrt{\frac{\% successes \times \% failures}{\text{sample size}}} = \sqrt{\frac{\hat{p}(1 - \hat{p})}{n}}$$
Means
Sample Mean
$$\bar{X} = \frac{\text{sum of all observations}}{\text{sample size}} = \frac{x_1 + x_2 + \dots + x_n}{n}$$
Standard Error
$$SE_\bar{X} = \frac{\text{sample std dev}}{\text{factor of sample size}} = \frac{s_x}{\sqrt{n}}$$
A Note on the sqrt(n)’s
Both Standard Errors listed above are measures of variation on the center statistic of the distribution
Let’s do a quick derivation on why this works.
If x1, x2, … , xn are independent from a population w/ mean and stdev $\mu, \sigma$ then the variance of their total is
$$n\sigma^{2}$$
And because the sample mean is expressed as
$$\bar{X} = \frac{x_1, x_2, \dots, x_n}{n}$$
We can substitute that into the variance calculation
$$ Var(\bar{X}) = Var(\frac{1}{n}\sum\limits_{i=1}^{n}X_i)$$
$$= \frac{1}{n^2}\sum\limits_{i=1}^{n}Var(X_i)$$
$$= \frac{1}{n^2}n^2\sigma^2\frac{1}{n}$$
$$= \frac{\sigma^2}{n} $$
Thus, the standard deviation of this becomes $\frac{\sigma}{\sqrt{n}}$