Convolution Hyperparameters
Motivation
Our initial convolution intuition was built on the notion of a filter that scanned over an image extracting relevant features and reducing dimensionality into the next layers.
from IPython.display import Image
Image('images/conv_sliding.png')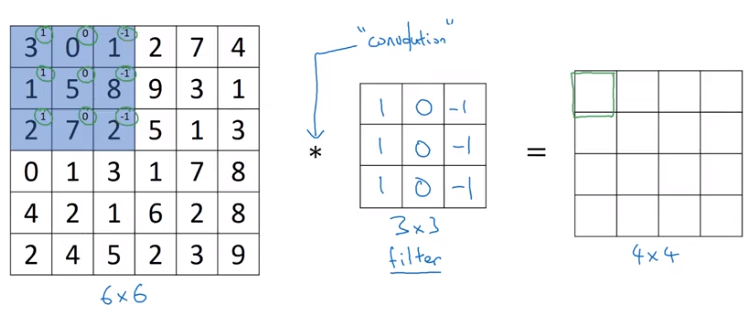
However, applying similar filters in subsequent layers would create a telescoping effect where basically hack-and-slash away at the dimension of our data until there’s nothing left in the final layers.
Thankfully, there are hyperparameters we can employ to correct for this.
Padding
By padding the outside of our original image with a bunch of zeros, we can fit more unique windows of the same size in our vertical and horizontal passes.
This still gives us all of the same information as before, but also has the added benefit of letting us use information found at the edges of our image, too.
Image('images/padding.png')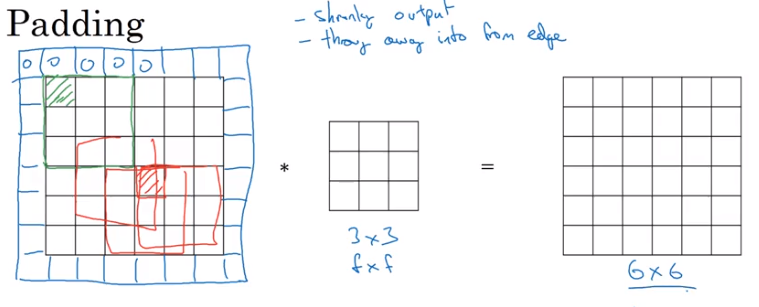
There are two types of filter padding schemes:
- Valid: Any value
f < nthat allows us to scan over the data - Same: Pad so that the output size is the same as the input size
To achieve Same padding, we want to choose pad value equal to
$p = \frac{f-1}{2}$
Stride
The other lever we can pull to adjust the size of our convolution output is stride, or the step size that we use when traversing the image vertically and horizontally with our filter.
Obviously a bigger stride means that we’ve got less room to move about, thus resulting in a smaller output-shape of our convolution.
Output Shape
Generally, given
n, the input shapep, paddingf, the size of your filters, stride
we can calculate the z x z dimension of our output shape with the following
$\lfloor \frac{n+2p-f}{s} + 1 \rfloor$
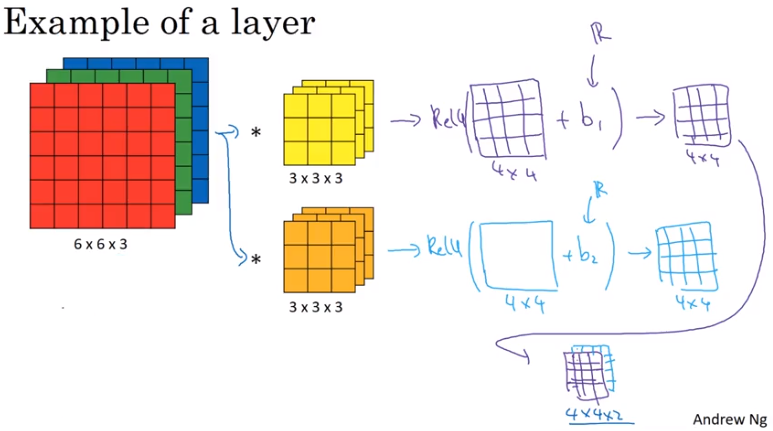
Multiple Filters
Lastly, we can create multiple filters to try and discern different features from our original image. They both do their convolution steps independently, then are concatenated into a multi-dimensional matrix before getting passed into the next layer.
Remember– you must ensure that the final dimension of your filters are compatible with your input data.
Image('images/conv_layers.png')